Беларуская Савецкая Энцыклапедыя (1969—76, паказальнікі; правапіс да 2008 г., часткова)
Verbum
анлайнавы слоўнікфіксуе залежнасць паміж аб’ёмам і зместам паняццяў: чым шырэйшы аб’ём паняцця, тым вузейшы яго змест, і наадварот. Калі аб’ём аднаго паняцця складае частку аб’ёму другога, то для іх зместу ўласцівыя адваротныя адносіны. Прынята лічыць, што першае вызначэнне гэтага закону належыць логікам Пор-Раяля (1660-я
У.Ф.Бяркоў.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
ЛАГАРЫФМАВА́ННЕ,
дзеянне, якое зводзіцца да адшукання лагарыфма лікавага,
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
АДВАРО́ТНЫЯ ТРЫГАНАМЕТРЫ́ЧНЫЯ ФУ́НКЦЫІ,
функцыі, якія вызначаюць дугу (лік) па дадзеным значэнні яе трыганаметрычных функцый, што разглядаюцца на пэўных прамежках манатоннасці.
Адрозніваюць («арксінус x») — мноства функцый,

Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
БАРЗДО́Ў Георгій Мікалаевіч
(
Тв.:
Эволюционные операторы электромагнитных волн в кристаллах. Ч. 1—3 // Кристаллография. 1990. Т. 35,
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
БАРКО́ЎСКІ Леанід Мацвеевіч
(
Тв.:
О тензоре показателей преломления в кристаллооптике // Кристаллография. 1976. Т. 21. № 3;
Операторы Коши и лучевые операторы в геометрооптике анизотропных сред (разам з Фо Тхі Нгует Хангам) // Оптика и спектроскопия. 1991. Т. 70. № 1.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
АДВАРО́ТНАЯ ФУ́НКЦЫЯ да функцыі y=, функцыя x=φ(y), што атрымліваецца з зададзенай функцыі , калі з ўраўнення =y выразіць x праз y.
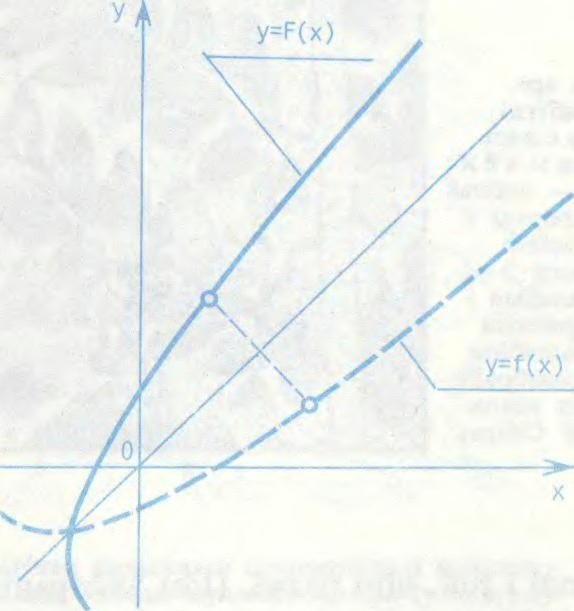
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
БІЯЛАГІ́ЧНЫЯ СІСТЭ́МЫ , сукупнасць узаемазвязаных і ўзаемадзейных жывых элементаў рознай складанасці (гены, клеткі, тканкі, органы, арганізмы, біяцэнозы, экасістэмы, біясфера). Валодаюць уласцівасцямі цэласнасці, адноснай устойлівасці, а таксама здольнасцю адаптацыі да зменлівых умоў навакольнага асяроддзя, развіцця, самаўзнаўлення і эвалюцыі. Біялагічныя сістэмы — адкрытыя сістэмы, для якіх умовай існавання служыць абмен энергіяй, рэчывам і інфармацыяй паміж часткамі сістэмы і з навакольным асяроддзем. Важнейшая праблема ў вывучэнні біялагічных сістэм — іх прасторавая і часавая арганізацыя, якая прадугледжвае ўключэнне ў сістэму некалькіх элементаў (больш за адзін), што адрозніваюцца пэўным наборам камплементарных паміж сабой прыкмет, на аснове чаго грунтуюцца ўзаемаадносіны паміж элементамі і забяспечваецца ўстойлівасць сістэмы. Тэорыя інфармацыі дазваляе ўвесці колькасныя ацэнкі ўзроўню арганізацыі, што забяспечваецца множнасцю, ступенню разнастайнасці элементаў і сувязяў паміж імі. На гэтай аснове адрозніваюць дэтэрмінаваныя, імаверныя і хаатычныя сістэмы. Біялагічныя сістэмы захоўваюць сваю спецыфічнасць у зменлівых умовах асяроддзя. Іх іерархічнасць і самарэгуляцыя забяспечваюцца шматузроўневым кіраваннем на аснове
А.С.Леанцюк.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)