Verbum

БЕЗРАЗМЕ́РНАЯ ВЕЛІЧЫНЯ́,

вытворная фізічная велічыня, не залежная ад змены ў аднолькавую колькасць разоў велічыняў, выбраных за асноўныя. У сістэме велічыні, дзе за асн. выбраны даўжыня L, маса M і час T, размернасць некаторай безразмернай велічыні х роўная 1, г. зн. dim x = L°M°T° = 1 (усе паказчыкі размернасці такой велічыні роўныя нулю). Напрыклад, цэнтр. плоскі вугал, абмежаваны двума радыусамі акружнасці, не залежыць ад даўжыні радыуса і ў сістэме велічынь LMT будзе безразмернай велічынёй. Да безразмерных велічынь належаць усе адносныя велічыні: адносная шчыльнасць, адноснае падаўжэнне, адносныя дыэлектрычная і магн. пранікальнасці і інш. Безразмерная велічыня ў адной сістэме велічыняў можа быць размернай у іншай сістэме.

т. 2, с. 374

ВЫ́ПУКЛАСЦЬ І ЎВАГНУ́ТАСЦЬ крывой, уласцівасць крывой, калі ўсе пункты любой яе дугі ляжаць не вышэй (не ніжэй) за хорду, якая сцягвае гэтую дугу. Пункт, у якім выпукласць крывой пераходзіць ва ўвагнутасць, наз. пунктам перагіну. Напр., крывая y=sin x увагнутая ў інтэрвале (0, π), выпуклая ў інтэрвале (π, 2π), пункт перагіну x=π.

Калі функцыя $𝑓\text{(}x\text{)}$ мае першую і другую вытворныя, то выпукласць і ўвагнутасць можна ахарактарызаваць так: у пунктах выпукласці крывая ляжыць не ніжэй за датычную і другая вытворная f″(x) > 0, у пунктах увагнутасці — не вышэй за датычную і f″(x) < 0 (калі f″(x) = 0, патрабуюцца дадатковыя даследаванні). Аналагічна вызначаецца выпукласць і ўвагнутасць паверхняў. Вобласць (частка плоскасці або прасторы), якая абмежавана выпуклай крывой (або выпуклай паверхняй), наз. выпуклай. Уласцівасці выпуклых абласцей вывучаюцца ў геаметрыі выпуклага цела.

В.В.Гарохавік.

т. 4, с. 319

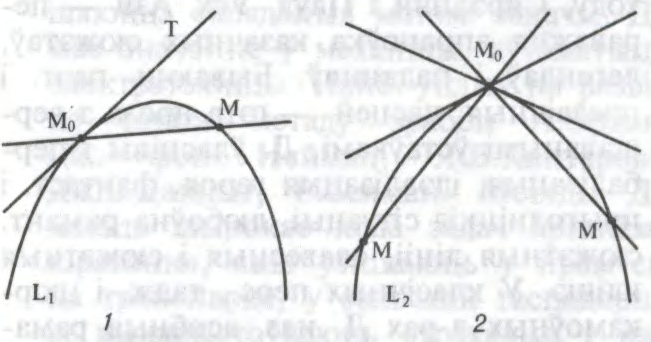
ДАТЫ́ЧНАЯ ПРАМА́Я да крывой лініі,

лімітнае становішча адпаведнай сякучай.

Няхай М₀ — зафіксаваны пункт крывой l, М — іншы яе пункт. М₀М — сякучая (прамая, праведзеная праз гэтыя пункты). Калі пры неабмежаваным набліжэнні М да М₀ сякучая М₀М імкнецца да пэўнай прамой М₀Т, то прамая М₀Т наз. Д.п. да крывой l у пункце М₀. У выпадку плоскай крывой, вызначанай у дэкартавых каардынатах ураўненнем y=f(x), дзе f(x) — дыферэнцавальная функцыя, ураўненне Д.п. да яе ў пункце М₀(x₀, y₀) мае выгляд y−y₀=f′(x₀) (x−x₀), дзе f′(x) —вытворная функцыя f′(x) у пункце x₀. Д.п. ўтварае з дадатным напрамкам восі OX вугал, тангенс якога роўны f′(x). Д.п. мае не кожная неперарыўная крывая, паколькі прамая M₀M можа і не імкнуцца да лімітнага становішча або можа імкнуцца да двух розных лімітных становішчаў, калі М імкнецца да M₀ з розных бакоў ад M₀.

А.А.Гусак.

т. 6, с. 62

ГРАВІТАЦЫ́ЙНАЕ ПО́ЛЕ ЗЯМЛІ́,

поле сілы цяжару, сілавое поле, абумоўленае гравітацыйным прыцяжэннем Зямлі і цэнтрабежнай сілай, выкліканай яе сутачным вярчэннем. Нязначнае ўздзеянне на гравітацыйнае поле Зямлі аказвае таксама прыцяжэнне Месяца, Сонца, планет Сонечнай сістэмы і масы зямной атмасферы. Характарызуецца вытворнымі патэнцыялу сілы цяжару па нармалі (па адвеснай лініі) да геоіда і па каардынатных восях у кожным пункце зямной паверхні. Вытворная патэнцыялу сілы цяжару па нармалі да геоіда вызначае паскарэнне свабоднага падзення, якое вымяраецца ў галах (1 Гал = 1 см/с​²). Адрозніваюць гравітацыйнае поле Зямлі: нармальнае, анамальнае і варыяцыі.

Нармальнае гравітацыйнае поле Зямлі абумоўлена прыцягненнем масы аднароднага эліпсоіда, паверхня якога блізкая да геоіда. Вагаецца ад 978 Гал на экватары да 983 Гал на полюсах. Анамальнае гравітацыйнае поле Зямлі выклікана неаднароднасцямі будовы Зямлі, гал. ч. яе верхняй абалонкі — літасферы. На раўнінных месцах знаходзіцца ў межах некалькіх дзесяткаў мілігал, у гарах і на астравах акіянаў анамаліі могуць дасягаць сотняў мілігал. Варыяцыі гравітацыйнага поля Зямлі ў часе звязаны з размяшчэннем Месяца адносна Зямлі і Зямлі адносна Сонца, а таксама з тэктона-фіз. працэсамі, што працякаюць на вял. глыбінях у нетрах Зямлі. Месячна-сонечныя перыядычныя варыяцыі гравітацыйнага поля Зямлі ў часе — да 1 мГал, варыяцыі поля тэктанічнага паходжання — 1—2 мГал за год. Гл. таксама Гравіметрыя.

Г.І.Каратаеў.

т. 5, с. 383

АНАЛІТЫ́ЧНАЯ ФУ́НКЦЫЯ,

функцыя, значэнне якой у кожным пункце яе вобласці вызначэння роўнае суме ступеннага шэрага, які збягаецца ў некаторым наваколлі гэтага пункта. Да аналітычнай функцыі адносяцца: рацыянальная функцыя, паказнікавая функцыя, лагарыфмічная функцыя, трыганаметрычныя функцыі, адваротныя трыганаметрычныя функцыі, іх разнастайныя кампазіцыі, а таксама функцыі, адваротныя да гэтых кампазіцый. Існуюць аналітычныя функцыі аднаго або некалькіх рэчаісных ці камплексных пераменных. Функцыя 𝑓(z) аднаго комплекснага пераменнага z=x+iy наз. аналітычнай функцыяй у пункце z₀, калі ў некаторым наваколлі h гэтага пункта існуе канечная вытворная $\mathrm{f}\text{′(}\mathrm{z}\text{)}=\underset{\mathrm{h}\to 0}{\overset{}{lim}}\frac{\mathrm{f}\text{(}\mathrm{z}+\mathrm{h}\text{)}-\mathrm{f}\text{(}\mathrm{z}\text{)}}{\mathrm{h}}$ (дыферэнцыравальнасць функцыі), што мае месца ў тым і толькі ў тым выпадку, калі выконваецца ўмова Кашы—Рымана $\frac{\mathrm{dt}}{\mathrm{dz̅}}=0$ , дзе $\mathrm{z̅}=\mathrm{x}+\mathrm{y}$. Асновы тэорыі аналітычнай функцыі былі закладзены А.Кашы, Б.Рыманам і К.Веерштрасам, С.В.Кавалеўскай і інш. На Беларусі даследаванні па тэорыі аналітычнай функцыі пачаліся ў 1930-я г. ў БДУ (М.В.Ламбін, М.Л.Лукомская), з 1960-х г. праводзяцца ў АН, БДУ і інш. ВНУ рэспублікі (Ф.Дз.Гахаў, Э.І.Звяровіч і інш.). Аналітычныя функцыі маюць шматлікія дастасаванні ў матэм. аналізе (вылічэнне вызначаных інтэгралаў), у геаметрыі (канформныя адлюстраванні), у тэорыі пругкасці, гідрадынаміцы, электрадынаміцы і інш. навуках. Гл. таксама Кашы інтэграл, Кашы тэарэма.

Літ.:

Маркушевич А.И. Теория аналитических функций. Т. 1—2. М., 1967—68;

Шабат Б.В. Введение в комплексный анализ. Ч. 1—2. 3 изд. М., 1985;

Гахов Ф.Д. Краевые задачи. 3 изд. М., 1977.

Э.І.Звяровіч.

т. 1, с. 335