ВЕЙНЯРО́ВІЧ (Іосіф Навумавіч) (
Літ.:
Бондарева Е.Л. В кадре и за кадром.
Р.З.Ясінскі.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
ВЕЙНЯРО́ВІЧ (Іосіф Навумавіч) (
Літ.:
Бондарева Е.Л. В кадре и за кадром.
Р.З.Ясінскі.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
МІКАЛА́Й КУЗА́НСКІ [Nicolaus Cusanus;
нямецкі філосаф, багаслоў,
П.:
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
ДАТЫ́ЧНАЯ ПЛО́СКАСЦЬ
плоскасць, у якой ляжыць датычная прамая да кожнай лініі на паверхні, праведзенай праз гэты пункт.
Калі паверхня вызначана ўраўненнем F(x, y, z) = 0, дзе F(x, y, z) — дыферэнцавальная функцыя, ураўненне Д.
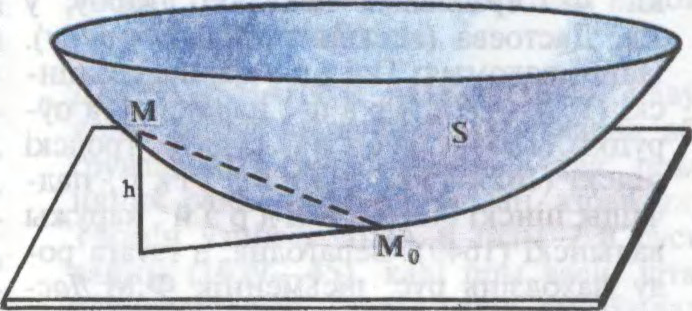
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
ГАРМАНІ́ЧНЫ АНА́ЛІЗ,
раздзел матэматыкі, у якім вывучаецца раскладанне функцый у трыганаметрычныя шэрагі і інтэгралы. Класічны гарманічны аналіз узнік у 18—19
Сутнасць класічнага гарманічнага аналізу ў раскладанні перыядычных функцый у збежныя Фур’е шэрагі, каэфіцыенты якіх у некат. выпадках вылічаюцца па Эйлера—Фур’е формулах, калі функцыя зададзена складаным выразам, табліцай або графікам — лікавымі, графічнымі і
Літ.:
Серебренников М.Г. Гармонический анализ.
Гусак А.А. Высшая математика. Т. 2. 2 изд.
А.А.Гусак.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
ГРАВІТАЦЫ́ЙНАЕ ЎЗАЕМАДЗЕ́ЯННЕ,
адзін з тыпаў фундаментальных узаемадзеянняў (разам з моцным,
У гравітацыйным узаемадзеянні ўдзельнічаюць усе класы элементарных часціц (
М.М.Касцюковіч.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
НАТУРФІЛАСО́ФІЯ (ад
філасофія прыроды, абстрактнае тлумачэнне прыроды, якая разглядаецца ў яе цэласнасці. Узнікла ў антычнасці, ёй быў уласцівы наіўны непадмацаваны
Т.І.Адула.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
ГЕАМЕТРЫ́ЧНАЯ О́ПТЫКА,
раздзел оптыкі, які вывучае законы распаўсюджвання святла на аснове ўяўлення пра светлавыя прамяні як лініі, уздоўж якіх перамяшчаецца светлавая энергія. У аднародным асяроддзі прамяні прамалінейныя, у неаднародным скрыўляюцца, на паверхні раздзела розных асяроддзяў мяняюць свой напрамак паводле законаў пераламлення і адбіцця святла. Асноўныя законы геаметрычнай оптыкі вынікаюць з Максвела ўраўненняў, калі даўжыня светлавой хвалі значна меншая за памеры дэталей і неаднароднасцей, праз якія праходзіць святло; гэтыя законы фармулююцца на аснове Ферма прынцыпу.
Уяўленне пра светлавыя прамяні ўзнікла ў
Літ.:
Слюсарев Г.Г. Методы расчета оптических систем. 2 изд. Л., 1969;
Борн М., Вольф Э. Основы оптики:
Вычислительная оптика: Справ. Л., 1984.
Ф.К.Руткоўскі.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)
ГЕАМЕ́ТРЫЯ (ад геа... + ...метрыя),
раздзел матэматыкі, які вывучае прасторавыя дачыненні і формы цел, а таксама
На Беларусі станаўленне геаметрыі пачалося ў 1930-я
Літ.:
Александров А.Д., Нецветаев Н.Ю. Геометрия. М., 1990;
Алгебра и аналитическая геометрия. Ч. 1.
Дифференциальная геометрия.
Феденко А.С. Пространства с симметриями.
А.А.Гусак.
Беларуская Энцыклапедыя (1996—2004, правапіс да 2008 г., часткова)