Verbum

рацыянальная функцыя

т. 13, с. 383

ступенная функцыя

т. 15, с. 223

трансцэндэнтная функцыя

т. 15, с. 513

характарыстычная функцыя

т. 16, с. 543

хвалевая функцыя

т. 16, с. 569

цеплавая функцыя

т. 17, с. 101

цэлая функцыя

т. 17, с. 161

ПАКА́ЗНІКАВАЯ ФУ́НКЦЫЯ, экспаненцыяльная функцыя,

функцыя y = e​^z = exp z, дзе e = 2,718... — аснова натуральных лагарыфмаў. П.ф. y > 0 пры любых сапраўдных значэннях z, а ў камплекснай вобласці прымае ўсе камплексныя значэнні, акрамя нуля. Графік П.ф. наз. экспанентай. Адваротнай П.ф. з’яўляецца лагарыфмічная функцыя. У курсе матэм. аналізу разглядаецца П.ф. віду y = a​^x пры сапраўдных x і дадатных a, якая звязана з асн. П.ф. суадносінамі a​^x = e​^xlna. П.ф. сустракаецца ў дастасаваннях, дзе скорасць змены якой-н. велічыні прама прапарцыянальная самой велічыні, напр., пры апісанні працэсу радыеактыўнага распаду, затухання ваганняў.

т. 11, с. 523

экспаненцыяльная функцыя

т. 18, кн. 1, с. 75

ЛІНЕ́ЙНАЯ ФУ́НКЦЫЯ,

функцыя выгляду $y=kx+b$ , дзе k і b — сапраўдныя лікі. Асн. ўласцівасць: прырашчэнне функцый прапарцыянальнае прырашчэнню аргумента.

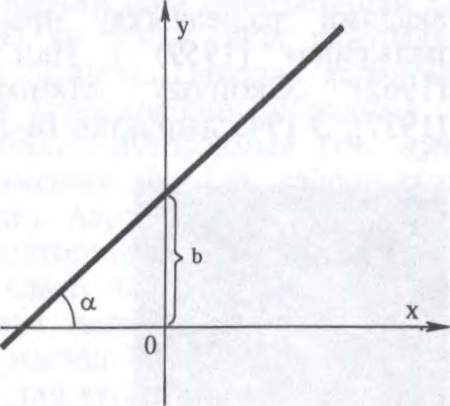
Графік Л.ф. на плоскасці xOy — прамая лінія, пры гэтым b — ардыната пункта перасячэння графіка Л.ф. з воссю Oy, $k=tg\mathrm{\alpha }$ , дзе α — вугал паміж гэтай прамой і воссю Ox. Л.ф. выкарыстоўваецца ў фізіцы і тэхніцы, каб паказаць залежнасць паміж прама прапарцыянальнымі велічынямі.

т. 9, с. 267