Verbum

АКУПА́ЦЫЯ (ад лац. occupatio захоп) ваенная, у міжнар. праве часовы захоп тэрыторыі адной дзяржавы войскамі другой і ўстанаўленне ваен. адміністрацыі для кіравання ёю. Рэжым акупацыі рэгулюецца 4-й Гаагскай канвенцыяй 1907 пра законы і звычаі сухапутнай вайны, Жэнеўскай канвенцыяй 1949 пра абарону цывільнага насельніцтва ў час вайны і дадатковым пратаколам 1977 да яе. Паводле гэтых пагадненняў акупацыйныя ўлады абавязаны падтрымліваць грамадскі парадак і ствараць нармальныя ўмовы для пражывання насельніцтва. У практыцы 1-й і 2-й сусв. войнаў вядомы шматлікія факты грубага парушэння Германіяй і яе саюзнікамі нормаў міжнар. права, найперш у адносінах да мірнага насельніцтва, якое станавілася аб’ектам жорсткага падаўлення і знішчэння. Рэжым пасляваеннай акупацыі звычайна ўстанаўліваецца спец. міжнар. пагадненнямі зацікаўленых дзяржаў для пэўнай дзяржавы або тэрыторыі з мэтаю выканання ўмоў мірнага дагавору.

Л.В.Паўлава.

т. 1, с. 218

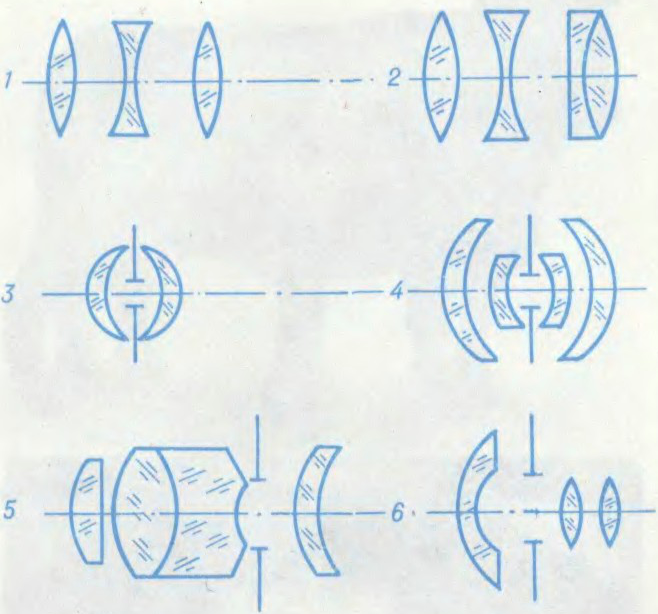
АБ’ЕКТЫ́Ў,

аптычная сістэма або яе частка, якая стварае сапраўдны адваротны відарыс аб’екта. Створаны аб’ектывам відарыс разглядаецца праз акуляр (звычайна пасля абарачальнай сістэмы) ці фіксуецца на экране, фатагр. плёнцы, фотакатодзе перадавальнай тэлевізійнай трубкі і інш. Бываюць лінзавыя, люстраныя і люстрана-лінзавыя.

Асн. аптычныя характарыстыкі: фокусная адлегласць f; дыяметр уваходнай зрэнкі d; святласіла d/f; вугал (поле) зроку; раздзяляльная здольнасць. Аб’ектывы тэлескапічных сістэм маюць фокусную адлегласць да некалькіх метраў і дыяметр уваходнай зрэнкі ад некалькіх сантыметраў (у геад., вымяральных і падзорных трубах) да некалькіх метраў (у тэлескопах-рэфрактарах), аб’ектывы мікраскопаў — фокусную адлегласць 1,5—40 мм, малафарматных фотаапаратаў — 6—2000 мм (для аматарскай практыкі 28—200 мм). Фатагр. аб’ектывы бываюць нармальныя (вугал зроку 40—50°), шырокавугольныя (больш за 70°), звышшырокавугольныя (больш за 83°, аб’ектывы тыпу «рыбіна вока» больш за 180°), даўгафокусныя (менш за 39°) і звышдаўгафокусныя (менш за 9°). Канструкцыя складаных аб’ектываў дазваляе выправіць храматычную і геам. аберацыі аптычных сістэм. Большасць аб’ектываў — анастыгматы. Аб’ектывы з пераменнай фокуснай адлегласцю (панкратычныя), у якіх плоскасць відарыса і святласіла нязменныя, выкарыстоўваюцца ў кіна- і тэлекамерах, спец. прамянёвастойкія — у лазерных сістэмах. Для павелічэння фіз. святласілы аб’ектывы прасвятляюць (гл. Прасвятленне оптыкі).

В.В.Валяўка.

т. 1, с. 19

А́ЛГЕБРА ЛО́ГІКІ,

раздзел матэматычнай логікі, які вывучае логікавыя аперацыі над выказваннямі. Заснавальнік — англ. матэматык Дж.Буль (1815—64). Алгебра логікі разглядае выказванні толькі з пункту гледжання іх праўдзівасці (пазначаюць лічбамі 1 — праўдзівасць і 0 — ілжывасць). Логікавыя аперацыі над выказваннямі даюць магчымасць будаваць новыя выказванні. Праўдзіваснае значэнне такога выказвання A (a₁,..., a_n), атрыманага пры дапамозе логікавых аперацый з прасцейшых выказванняў a₁, ..., a_n, адназначна выяўляецца праўдзіваснымі значэннямі зыходных выказванняў a₁,..., a_n. Таму кожнаму такому выказванню A (a₁, ..., a_n) адпавядае n-ме́сцавая функцыя, якая прымае значэнні 0,1, аргументы яе таксама прымаюць гэтыя значэнні. Такія функцыі наз. функцыямі алгебры логікі, ці булевымі, функцыямі. Яны могуць быць зададзеныя з дапамогай праўдзівасных табліц, якія маюць 2​ⁿ радкоў.

Логікавыя аперацыі: кан’юнкцыя &, дыз’юнкцыя ⋁, адмаўленне ¬, імплікацыя ⇒, эквіваленцыя ⇔ — могуць быць зададзеныя з дапамогай праўдзівасных табліц. Замест ¬x часам пішуць x̅. Ужываецца заданне функцый алгебры логікі і з дапамогай формул у мове, у якой ёсць пераменныя x, y, z... і сімвалы некаторых канкрэтных функцый. Найбольш ужывальная мова, якая мае логікавыя сімвалы &, ⋁, ¬, ⇒, ⇔. Кожнай формуле гэтай мовы адпавядае нейкая функцыя алгебры логікі, значэнне (0,1) якой пры дадзеных значэннях пераменных (0,1) знаходзіцца ў адпаведнасці з аперацыямі, з якіх пабудавана дадзеная формула. Такая функцыя рэалізуе дадзеную формулу. Формулы A і B наз. роўнымі (раўназначнымі), калі адпаведныя ім функцыі роўныя, г.зн. калі супадаюць іх праўдзівасныя табліцы. Азначэнне A=B ці A≡B, A~B, калі кажуць пра іх раўназначнасць. Важную ролю ў алгебры логікі маюць роўнасці, якія задаюць булеву алгебру.

Кожная функцыя алгебры логікі можа быць рэалізаваная нейкай формулай мовы з логікавымі сімваламі &, ⋁, ¬. Асаблівую ролю ў алгебры логікі адыгрываюць дыз’юнктыўныя і кан’юнктыўныя нармальныя формы, якія маюць вял. прыкладное значэнне. Сістэма функцый Ф. наз. функцыянальна поўнай, калі адвольная функцыя алгебры логікі можа быць рэалізаваная формулай, якая мае толькі сімвалы функцый з Ф. Напр., сістэмы функцый {&, ⋁, ¬}, {&, ¬}, {⋁, ¬}, {⇒, ¬}, {x | у}, {x ↓ у} функцыянальна поўныя (тут $\mathrm{x}|\mathrm{y}=\mathrm{x}\&\mathrm{y}\_$ , $\mathrm{x}\downarrow \mathrm{y}=\mathrm{x}\bigvee \mathrm{y}$ , якія наз. штрыхам Шэфера і стрэлкай Пірса адпаведна).

Алгебра логікі мае шмат дадаткаў, асабліва ў тэорыі эл. схем.

Р.Т.Вальвачоў.

т. 1, с. 234